Binary Options Greeks

The fair price of options can be theoretically calculated using a mathematical equation, which is commonly referred to as Black-Scholes model (BSM). The variables in the BSM are represented by the Greek alphabets. Thus, the variables are called as option Greeks. By monitoring the changes in the value of option Greeks, a trader can calculate the changes in the value of an option contract.

Collectively, there are five option Greeks, which measures the price sensitivity of an options contract in relation to four different factors namely:

• Changes in the price of the underlying asset
• Interest rate
• Volatility
• Time decay

The five option Greeks, which a binary options trader should compulsorily familiarize, are as follows:

Delta

Delta, which is considered to be the most important variable among option Greeks, represents an option’s sensitivity to the changes in the price of an underlying asset. In other words, Delta or the hedge ratio reflects the quantum of change in the price of an option for a $1 change in the price of an underlying asset. Represented by the Greek symbol ‘δ’, the Delta can have both positive and negative values.

The Delta value does not remain fixed and changes as a function of other variables.

If the price of an underlying asset goes up, the price of a call option will go up as well (assuming negligible changes in other variables). For example, if the price of a stock is $10 and the option’s Delta value is 0.7 then for every dollar increase in the price of the underlying asset, the call price will go up by $0.70. Conversely, for every dollar decrease in the price of the asset, the call price will go down by $0.70.

On the other way round, considering the same example discussed above, a dollar increase in the price of an underlying asset will result in a decrease in the price of a put option by $0.70 and vice versa.

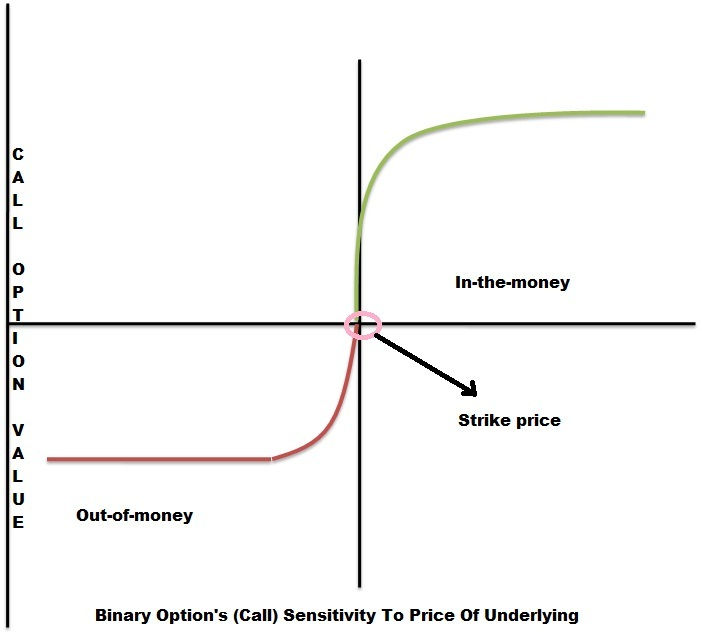
Now, let us consider binary options, which is a mathematical derivative of the vanilla options. Logically, at the beginning of a trade, a binary call or put nearest to the underlying price will have the highest Delta. The Delta value of a binary option can reach infinite a moment before the expiry thereby leading to a profit from the trade.

The Delta value for binary calls is always positive while the Delta value for binary puts is always negative.

Gamma

Earlier in this article, we have mentioned that Delta is a dynamic number, which undergoes changes along with changes in the price of a stock. The rate at which the value of Delta will change for a $1 change in the price of a stock is called the gamma.

Thus, it can be inferred that options with high gamma will respond faster to changes in the price of the underlying asset.

Let us consider that a call option has a Delta of 0.40. So, when the price of the underlying asset rises by $1, the call price would rise by $0.40. However, once the price of the options rise by $0.40, the Delta value is no longer 0.40. This is because the call option would be a little deeper in the money. Thus, the Delta will move closer to 1.0. Let us assume that the Delta is now 0.60.

The change in the Delta value, which is 0.20 (0.60–0.40), for a $1 change in the price of the underlying asset is the gamma value for the given options contract.

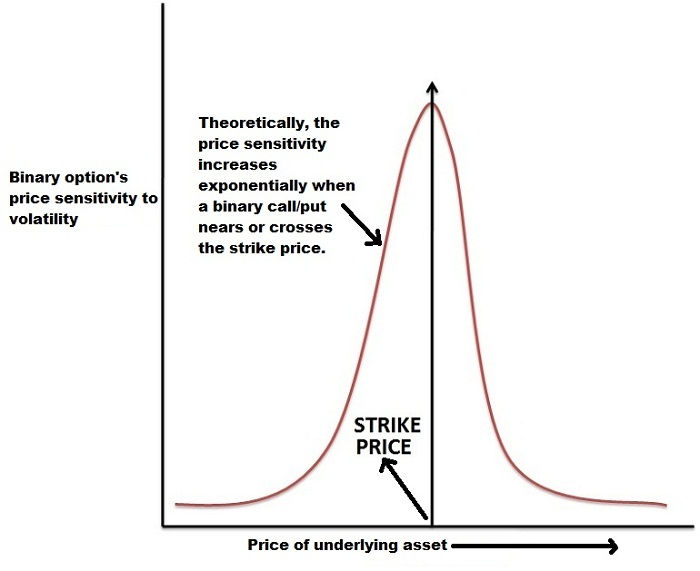
The Delta cannot exceed 1.0 as mentioned before. Thus, Gamma would decrease (turn negative) as option goes deeper in the money. Gamma, represented by the Greek alphabet ‘γ’, plays an important part in the change of Delta when a binary call/put option nears the target price. The Gamma rises sharply when a binary option nears or crosses the target. In short, Gamma acts as an indicator for the future value of Delta. Thus, it is a useful tool for hedging.

Theta

Theta, commonly referred to as time decay, would arguably be the most often discussed jargon by technical analysts. Theta, represented by Greek letter ‘θ’, refers to the amount by which the price of a call or put option would decrease corresponding to a single day change in the expiry time of an option contract.

The value of a call or put option decreases as each minute passes away. This means that even if the underlying price of an asset does not change, still, a call or put option will lose its entire value at the time of expiry. Theta factor is a must to consider while trading vanilla options.

In the case of binary options, as long as the price stays above the call price or below the put price, the trade will result in a profit. That being the case, the value of a binary call/put trade theoretically increases with the approach of the expiry time. The conventional call/put options, on the other hand, will lose their time value and trade at their intrinsic value.

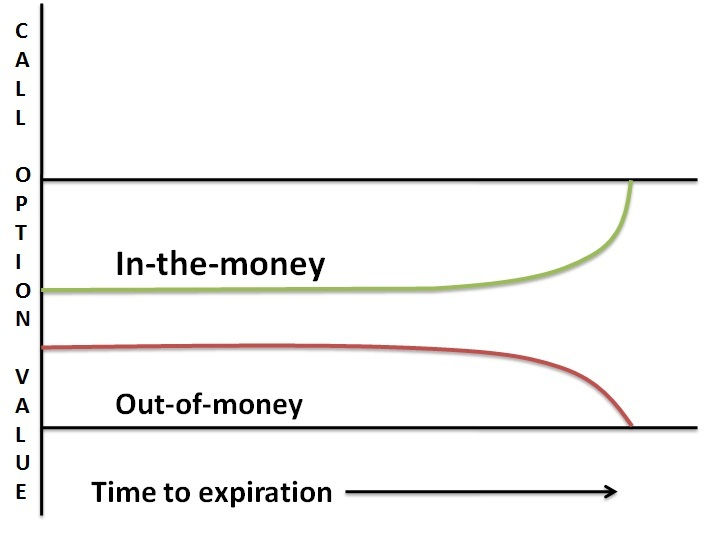
There are some binary brokers who allow traders to exit before expiry. In such cases, the payout percentage (when the trade is in-the-money) will generally increase as the expiry gets nearer. Such a ‘take profit’ facility is in line with the discussion above.

Vega

It is a well-known fact that implied volatility of no two assets traded in the financial markets is similar. Additionally, the implied volatility of any given asset does not remain constant. A change in the implied volatility of a security would cause a change, smaller or larger, in the price of a call or put option. Thus, Vega refers to the quantum of change seen in the price of a call or put option for a single point change in the implied volatility of the underlying asset.

Usually, an increase in the implied volatility results in a rise in the value of options. The reason is that higher volatility demands an increase in the range of potential price movement of an underlying asset. It should be noted that a call or put option with one year expiry period can have a Vega value of even up to 0.20.

Volatility is an enemy for a binary options trader in the sense that it can turn a profitable trade (in-the money) into a loss (out-of-money) at the moment of expiry. Thus, we can argue that high Vega is not preferable for a binary options trader.

Rho

Interest rates do have an impact on the price of call and put options. The change in the price of call and put options for a one point change in the interest rate is represented by the variable Rho. Short-term vanilla option players will not be affected by the value of Rho. Thus, analysts rarely speak about it. Only those traders who trade long-term options such as LEAPS are affected by Rho or the cost of carry.

Naturally, it can be understood that Rho, represented by the Greek alphabet ‘ρ’, is insignificant for a binary options trader since most of the binary option trades have relatively short-term expiry and no cost of carry is charged after entering a trade.

By managing the Delta, Gamma and Theta values efficiently, a trader can not only select trades properly but also achieve a desired risk to reward ratio. Additionally, the knowledge of options Greeks would enable a trader to create highly beneficial inter-market strategies in the long run.